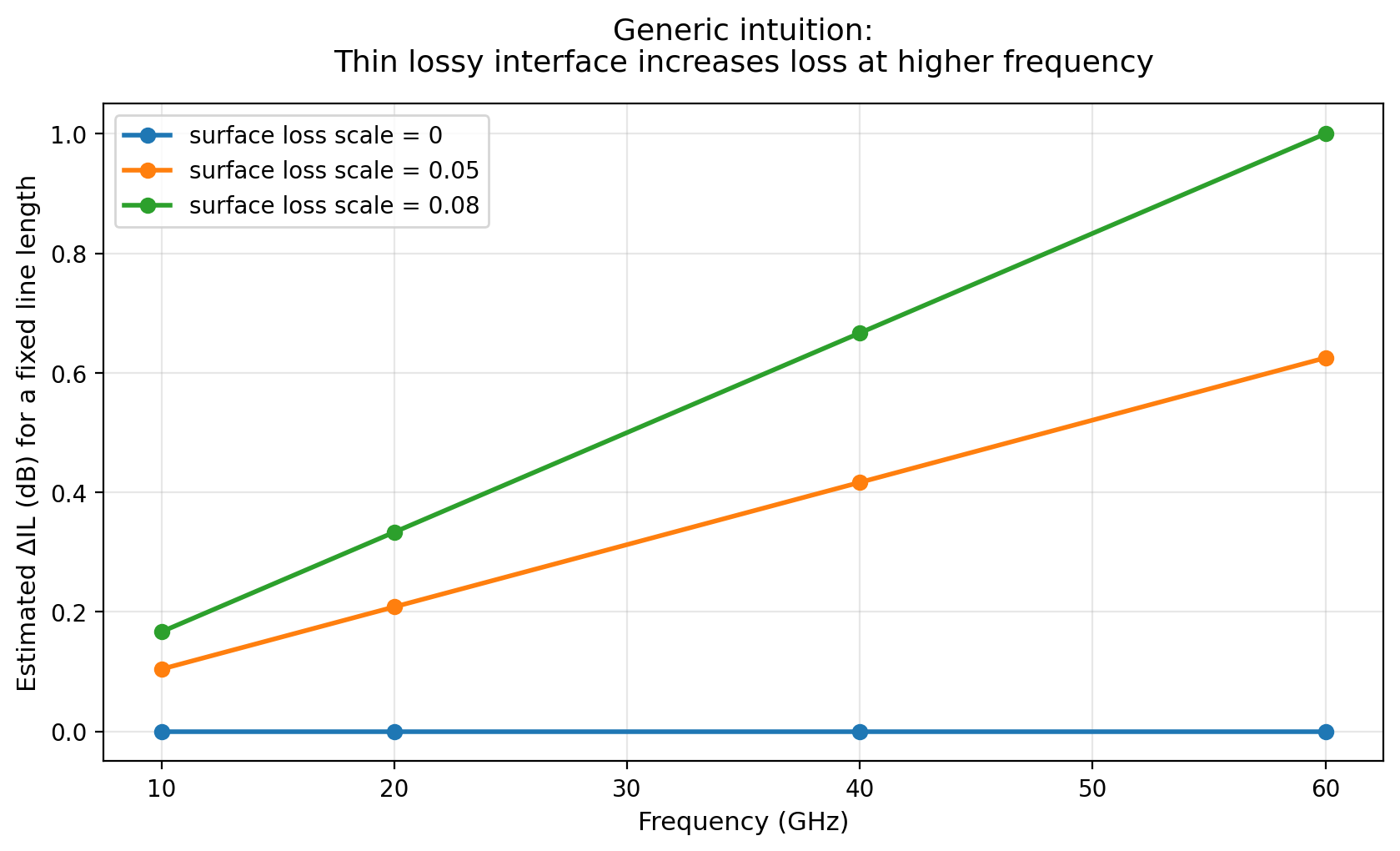
Example intuition plot (synthetic): a thin lossy interface can increase insertion loss more at higher frequency.
What this project teaches
- Field participation: where the electric field energy “lives” inside a layered stack.
- Why εr matters: increasing permittivity tends to pull energy into that layer.
- Why thin interfaces matter: even a thin lossy layer can dominate loss if the field concentrates there.
- Sensitivity mindset: sweeping assumptions is often more informative than a single “best guess.”
Why it matters
In layered RF/EM structures, the loss is rarely explained by one number. Real behavior comes from an interaction between geometry, material properties, and where the fields concentrate.
This project aims to provide a compact, visual intuition layer—so you can reason about trends before running expensive 3D simulations or measurements.
Modeling idea (high-level)
We treat the cross-section as a 2D electrostatic/quasi-TEM problem to estimate the potential V(x,y),
then compute E = -∇V. From that, we estimate energy participation in each region and map it into an
illustrative loss estimate versus frequency using simple dielectric/condutive loss assumptions.
Note: This page is a learning-oriented “intuition builder.”
How to remember the TEM / quasi-TEM relations
A transmission line behaves like a distributed LC ladder. The wave is slowed because it must continuously store electric energy (capacitance) and magnetic energy (inductance). Ratio gives impedance, product gives speed.
Z0 = sqrt(L′ / C′)
β = ω · sqrt(L′C′)
n_eff = c · sqrt(L′C′) = c / v_p
- Impedance is a ratio: more
L′makes current harder (higherZ0), moreC′stores voltage easier (lowerZ0). - Phase is frequency × slowness:
βgrows withωand withsqrt(L′C′)(more stored energy → slower wave). - Index is a speed penalty:
n_eff = c / v_p. BiggerL′C′→ smallerv_p→ largern_eff.
One-line mnemonic: “Impedance is root L over C; phase is ω times root LC; index is c times root LC.”